\mathstyle: [展開可能] 現在の数式スタイルを表す整数(の十進表記のトークン列)に展開される。
※「スタイル」の記号の意味については以前の記事を参照。値 0 1 2 3 4 5 6 7 −1 スタイル D D′ T T′ S S′ SS SS′ 非数式
某アドベントカレンダーの記事で詳しく解説していたように、TeX で「現在の数式スタイル」を判定する場合は(極めて不便な)\mathchoice プリミティブが使える。そして(極めて絶望的なことに)大概の TeX エンジンについてはそれが唯一の方法である。ところが LuaTeX ではもっと直接的に「現在の数式スタイル」が判定できる、だったらよかったのに、という話。
\mathstyle を使う話
\mathstyle プリミティブは、「現在の数式スタイル」が 8 つのうちの何れかに応じて 0〜7 の整数値を示す。数式外では −1 の値を示す。\mathstyle を利用して例えば次のようなマクロを作ることができる。
% \showMS: 現在の数式スタイルの情報を端末に表示する. \def\showMS{% \message{\ifcase\mathstyle\space D\or D'\or T\or T'\or S\or S'\or SS\or SS'\else X\fi}}
実際に「\showMS を用いて数式スタイルを調べる」例を示す。
% LuaTeX 文書 \input showms.def % さっきの \showMS マクロを使う \def\X{X\showMS}%"X"を書きつつ端末に情報表示 $\X^{\X^{\X}} \overline{\X}$ % 最後は'cramped'になるはず \bye
T S SS T'
組版結果は次の通り。
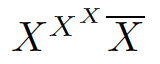
\displaystyle で整数する話
\mathstyle の仕様の便宜のため、LuaTeX では \displaystyle や \crampedtextstyle などの(8 つある)数式スタイル変更のプリミティブについて、各数式スタイルに対応する(上表にある)整数の定数として使えるようになっている。つまり次のような使い方ができる。
\ifnum\mathstyle=\textstyle (非crampedの)テキストスタイルである) \fi
補足
TeX において“整数値を返す”(関数のような)プリミティブ(\inputlineno や \lastpenalty 等)は大抵は「読取専用の整数パラメタ」の形で与えられることが多い。この場合、値を(数字として)表示するには \the を付ける必要がある。*2
\message{\the\lastlineno}
これに対して \mathstyle は「値の数字列に展開される」という性質をもち(pdfTeX の \pdfstrcmp や \pdffilesize も同様の性質をもつ)、“\def\five{5}”のように定義されたマクロと同じ挙動を示す。だから、値を表示するときには \the は不要である((\the を付けるとエラーになる。))。
\message{\mathstyle}
(表示するのでなく)単に整数として用いる場合、\mathstyle は明示的な数字列と同じ扱いになるため、一般的には \relax や空白(\space)で数字列を終結させる必要がある。((\showMS の定義では完全展開可能が要求されるので、\relax でなく \space を用いていることにも注意。))
\newcount\hoge \hoge=\inputlineno % 終結は不要 \hoge=\mathstyle\relax % 終結が必要
なお、「整数としての \displaystyle」は内部値である(そもそも「内部値として使われたときだけ整数として振舞う」という規則である)。
\mathstyle を使えない話
以上に述べた \mathstyle の性質を前提にすると、展開可能な場所に \mathstyle があった場合は“現在の数式スタイル”(に相当する数値)の数字に“その場”で展開される。さて、以前の記事を読んで「数式スタイルは“その場”では決まらない」ということを知っている人は、当然「どうしたらそんなことが可能なのか」という疑問を抱くことだろう。
これについて解説する前に、まず、「どういう場合に」数式スタイルが“その場で”決まらないのかについて述べておく。TeX の数式において、分数は次のように表される。((LaTeX では(その文法に整合するように)分数を“\frac{分子}{分母}”のように書くが、\frac 命令の実装は単に“{分子 \over 分母}”に展開するマクロになっている。plain TeX では分数を書くのに直接 \over を使う。))
{分子 \over 分母}
それでは次のような例を考えよう。((“{\cal A}”は LaTeX の“\mathcal{A}”と同等で、筆記体の A を出力する。))
$X = {\cal A\message{\mathstyle} } / 2$
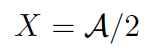
さて、ここで \mathstyle は何に展開されるべきだろうか。\mathstyle がある位置での数式スタイルは T なので答えは「2」である。ところがもし \mathstyle の後ろが次のようになっていたらどうだろうか。
$X = {\cal A\message{\mathstyle} \over \rm 2}$
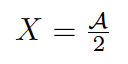
この場合、{...} の部分は分数であるので、\mathstyle の位置の数式スタイルは S であり、\mathstyle は「4」に展開されなければならない。ところが、この両者を比べると、\mathstyle が現れるより前の部分は全く同一であるので、この \mathstyle の展開が 2 と 4 の何れになるのかは判断がつかない。これが「現在の数式スタイルが“その場で”決まらない」の意味するところである。
TeX には \over の他にも“分数のようなもの”(二項係数とか平方剰余記号とか;「汎化分数(generalized fraction)」と呼ばれる)を組むためのプリミティブが幾つか用意されている。((amsmath パッケージの \genfrac 命令は汎化分数用プリミティブの幾つかを利用している。))
\over(=\abovewithdelims..<既定線幅>)\atop(=\abovewithdelims..0pt)\above<線幅>(=\abovewithdelims..)\overwithdelims(=\abovewithdelims<左><右><既定線幅>)\atopwithdelims<左><右>(=\abovewithdelims<左><右>0pt)\abovewithdelims<左><右><線幅>- この
\abovewithdelimsが最も汎用的な形式であり、前の 5 つはこれの“短縮系”である。 <左>・<右>は分数の左右に付ける括弧類(デリミタ)を指定する。「.」を指定すると括弧無しになる。<線幅>は分子と分母の間に引かれる横線の太さ。\overや\overwithdelimsでは“既定の線幅”が使用され、その値は数式フォントの種類により異なる。((詳しく言うと、数式ファミリ 3(通常は cmex10 などの大型演算子のフォントが割り当てられる)のフォントパラメタ 8 番の値に等しい。上線・下線(\overline・\underline)や根号(\root)で用いられる線の幅もこのパラメタに等しい。))10pt の CM フォントの場合 0.4pt。
- この
そして、\over と同様、汎化分数も「数式スタイルが“その場で”決まらない元凶」となる。逆に元凶となるものは汎化分数に限られるようである。
\mathstyle の現実の話
では当初の疑問に戻ろう。数式が汎化分数を含む場合、そのサブ数式の中に出現した \mathstyle はどうやって「正しい答えを得ている」のだろうか。これに対する正解は、実は驚くほど単純である。
正しい答えを得ていない。
このことは実際に試してみれば判る。
% plain LuaTeX 文書 \input showms.def \def\X{X\showMS} $\X = {\X \over \X}$ \bye
これをコンパイルすると端末の表示は次のようになる。
T T T'
もちろん正解は「T S S'」である。すなわち、\mathstyle は汎化分数のサブ数式の中では正しい情報を返さない、という「仕様」になっているのである。LuaTeX のマニュアルには次のように書かれている。
There are a few math commands in TeX where the style that will be used is not known straight from the start. These commands (\over,\atop,\overwithdelims,\atopwithdelims) would therefore normally return wrong values for\mathstyle. To fix this, LuaTeX introduces a special prefix command:\Ustack:(LuaTeX Refernce; 5.1.2 \Ustack)
そしてこれを見ると、“\Ustack”というプリミティブでこの誤った結果を“修正”できるとも書かれている。要するに、\mathstyle を扱う際には、\Ustack もセットで扱わないといけないのである。しかしこの記事はもうかなり長くなっているので、\Ustack の解説は次回の「きょうの LuaTeX」に回すことにしよう。