マクロツイーター

はてダから移行した記事の表示が崩れてますが、そのうちに直せればいいのに（えっ）

TeX で数式を生成する 〜アッカーマン関数編〜

TeX

……いや、「SATySFi Advent Calendar 2018」（参加者募集中！）の記事「SATySFiで数式を生成する 〜アッカーマン関数編〜」を読んで、何となく作りたくなったので。

目標

TeX で以下の命令（マクロ）を実装する。

方針

  • 元ネタで代数的データ型が使われているので、TeX で代数的データ型を扱う手法を利用する。
  • 特にその必要がないため、完全展開可能にはしない。「関数の返り値」の扱いは「特定の制御綴への代入」を採用する。
  • plain TeX と LaTeX の両方で通用するコードを書く。e-TeX 拡張は使わない。

式構造

式構造を表すデータは以下のトークン列で表す。

  • \my@Num{<n>}： 整数n
  • \my@Fun{<m>}{<n>}： Ack(m,n)

例えば、「Ack(2,8)」という式は \my@Fun{\my@Num{2}}{\my@Num{8}} で表される。

値を \edef で代入するときの便宜のため、以下のマクロを用意する。

%% 構築子
\def\my@@Num{\noexpand\my@Num}
\def\my@@Fun{\noexpand\my@Fun}

式を印字する

式を印字するための構築子の定義を与える。

\def\my@print@Num#1{#1}
\def\my@print@Fun#1#2{A(#1,#2)}

\my@use@print を実行すると実際の構築子の意味がこれらの定義に切り替わるようにする。

%% \my@use@print
% 式を印字する状態に移行する.
\def\my@use@print{%
  \let\my@Num\my@print@Num
  \let\my@Fun\my@print@Fun}

例えば、

\my@use@print $\my@Fun{\my@Num{2}}{\my@Num{8}}$

を実行すると以下の出力が得られる。

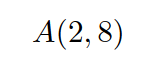
式が整数であるかを判定する

先の \my@use@isnum と同じ要領で構築子を定義する。真偽値を“返す”必要があるので、そのための変数を用意する。

\newif\ifmy@ok % 真偽値の返り値専用のスイッチ

%% \my@use@isnum
% "式が単なる整数であるか"を判定する状態に移行する.
% この状態で構築子を実行するとスイッチ my@ok に結果を返す.
\def\my@use@isnum{%
  \let\my@Num\my@isnum@Num
  \let\my@Fun\my@isnum@Fun}
\def\my@isnum@Num#1{\my@oktrue}
\def\my@isnum@Fun#1#2{\my@okfalse}

例えば次のようになる。

\my@use@isnum \my@Fun{\my@Num{2}}{\my@Num{8}}
\message{\ifmy@ok True\lese False\fi}
%→ False

式を一段評価する

次の仕様を満たす構築子のマクロ（\my@eval@...）を実装したい。

\let\my@ret\relax % トークン列返り値専用のマクロ

%% \my@use@eval
% 式を一段評価する状態に移行する.
% この状態で構築子を実行すると \my@ret に一段評価した結果の式を
% 表す値が代入される.
\def\my@use@eval{%
  \let\my@Num\my@eval@Num
  \let\my@Fun\my@eval@Fun}

例えば次のようになってほしい。

\my@use@eval \my@Fun{\my@Num{2}}{\my@Fun{\my@Num{8}}{\my@Num{0}}}
\message{\meaning\my@ret}
%→ macro:->\my@Fun{\my@Num{2}}{\my@Fun{\my@Num{7}}{\my@Num{1}}}
式が Num の場合

数値はそれ自身に評価されるので、次のようになる。

% 数値mの場合
\def\my@eval@Num#1{%{<m>}
  \def\my@ret{\my@Num{#1}}}
式が Fun の場合

「構築子の定義を切り替える」という方法で通すことも可能であるが、見通しが極めて悪くなるため、別の方法を考えることにする。

まず、構築子の名前（Num または Fun）を取り出す補助マクロを作る。

%% \my@name\my@XXX : 'XXX'に展開される.
\begingroup\lccode`\?=`\@ \lowercase{%
  \gdef\my@name#1{\expandafter\my@name@a\string#1;}
  \gdef\my@name@a#1?#2;{#2}
}\endgroup

その上で、引数の式の構築子が何であるかによって別のマクロに処理を委譲する。このとき、構築子の引数は委譲先のマクロの引数に渡す。

% Ack(X,Y)の場合 (X,Yは式)
\def\my@eval@Fun#1#2{%{<X>}{<Y>}
  \my@eval@Fun@a#1*;#2*;}% {}を外す
  %※'*'はダミーで, 後で除去される
\def\my@eval@Fun@a#1#2;#3#4;{%\X...*;\Y...*;
  \csname my@eval@Fun@@\my@name#1@\my@name#3\endcsname#2;#4;}

例えば、

\my@eval@Fun{\my@Num{2}}{\my@Fun{\my@Num{8}}{\my@Num{0}}}

を実行すると、結果的に次のトークン列が実行される。

\my@eval@Fun@@Num@Fun{2}*;{\my@Num{8}}{\my@Num{0}}*;

それでは、Fun の引数が両方とも Num である場合の処理（\my@eval@Fun@@Num@Num）を作ろう。

% 変数
\newcount\my@m
\newcount\my@mm
\newcount\my@n

% Ack(m,n)  (m,nは数値)
\def\my@eval@Fun@@Num@Num#1*;#2*;{%{<m>}*;{<n>}*;
  %※#1,#2の{}は外れるこに注意
  \my@m=#1\relax \my@n=#2\relax
  \ifnum\my@m=\z@ % Ack(0,_)
    \advance\my@n\@ne
    \edef\my@ret{\my@@Num{\the\my@n}}%
  \else\ifnum\my@n=\z@ % Ack(_,0)
    \advance\my@m\m@ne
    \edef\my@ret{\my@@Fun{\my@@Num{\the\my@m}}{\my@@Num{1}}}%
  \else % Ack(_,_)
    \my@mm\my@m \advance\my@m\m@ne \advance\my@n\m@ne
    \edef\my@ret{%
      \my@@Fun{\my@@Num{\the\my@m}}{%
        \my@@Fun{\my@@Num{\the\my@mm}}{\my@@Num{\the\my@n}}}}
  \fi\fi}

ここで、\my@ret に代入すべきトークン列を構成するのに、先ほど用意した \my@@... を利用している。例えば、\my@n が 8 のときに

\edef\my@ret{\my@@Num{\the\my@n}}%

を実行すると、\my@ret は \my@Num{8} となる。

次に、引数が (Num,Fun) である場合の処理を定義する。

\newtoks\my@toks

% Ack(m,Ack(X,Y))  (mは数値)
\def\my@eval@Fun@@Num@Fun#1*;#2#3*;{%{<m>}.;{<X>}{<Y>}*;
  % Ack(X,Y) の一段評価を求める(結果は \my@ret)
  \my@eval@Fun{#2}{#3}%
  % \my@ret の内容のトークン列を \my@toks に代入する
  \my@toks\expandafter{\my@ret}%
  \edef\my@ret{\my@@Fun{\my@@Num{#1}}{\the\my@toks}}}

\my@ret の内容を一旦トークン列レジスタに移しているのは、「edef 中でトークン列レジスタの参照はそれ以上展開されない」という性質を利用したいからである。もし、e-TeX 拡張の \unexpanded を使ってよいなら、最後の \my@ret の代入は次のように書ける。

% 中の \my@ret は一度だけ展開されてほしい
\edef\my@ret{\my@@Fun{\my@@Num{#1}}{\unexpanded\expandafter{\my@ret}}}

残りは引数が (Fun,Num) と (Fun,Fun) である場合であるが、実はこれの実装は不要である。なぜなら、評価の途中で Fun の第 1 引数が Fun になることは、実際には起こらないからである。従って、これまでのコードで \my@use@eval は完成である。

公開マクロ \Ack の実装

これは今までに作った部品を組み合わせるだけなので、特に難しいところはない。

%%<*> \Ack{<m>}{<n>}
% 公開マクロ.
\def\Ack#1#2{%
  % 元の式構造の値を \my@expr に代入.
  % (#1, #2の値を評価しておく.)
  \my@m=#1\relax \my@n=#2\relax
  \edef\my@expr{\my@@Fun{\my@@Num{\the\my@m}}{\my@@Num{\the\my@n}}}%
  % "(元の式)"を印字した結果を \my@box に入れる.
  \my@use@print \setbox\my@box\hbox{$\my@expr$}%
  % \my@expr を一段評価する.
  \my@use@eval \my@expr \let\my@expr\my@ret
  % 1行目"(元の式)=(今の式)"を印字する.
  \par\noindent \copy\my@box
  \my@use@print ${}=\my@expr$%
  \my@Ack@loop}
\def\my@Ack@loop{%
  % \my@expr を一段評価する.
  \my@use@eval \my@expr \let\my@expr\my@ret
  % "(今の式)"を左側の空きを入れて印字する.
  \par\noindent \hskip\wd\my@box
  \my@use@print ${}=\my@expr$%
  % 式構造がNumであるか検査する.
  \my@use@isnum \my@expr
  \ifmy@ok\else % Numでないならばループ
    \expandafter\my@Ack@loop
  \fi}

完成

以上のプログラムをプレアンブルに書いた上で、本体で \Ack{3}{1} を実行する LaTeX 文書を用意した。*1

これを LaTeX でコンパイルすると、Ack(3,1) の計算過程が印字された文書が得られる。

（1 ページ目先頭）
（3 ページ目先頭）

まとめ

というわけで、TeX 言語はアレなので、アッカーマン関数したい人は是非とも SATySFi を使いましょう！（えっ）

*1:えっ、パッケージに仕上げたほうがいいですか？;-)